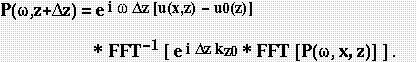(1)
Presented at the 1992 Annual SEG International Meeting, New Orleans, Louisiana.
This paper presents a modification to split-step Fourier migration which extends the accuracy of the method in handling severe lateral velocity variations. The modification results in a steep-dip post stack depth migration which is applicable in a wide range of geologic environments and which is economical to implement. Although similar to phase shift plus interpolation (PSPI) methods, the current algorithm avoids the additional computations and operator limitations of PSPI, making it ideal for steep dip imaging of three dimensional data sets. After describing the method, discussions are presented on program optimization and avoiding artifact contamination. Examples are included showing the migration impulse response in the presence of severe lateral velocity discontinuities, and the migration performance in imaging the flank of a salt diapir.
Migration methods that collapse diffractions in the frequency-wavenumber domain are usually classified as phase shift implementations. Within the petroleum industry, it is generally acknowledged that phase shift methods preserve steep dips and high frequencies better than finite difference implementations (Stolt, 1978). However, the difficulties associated with handling lateral velocity variations in f-k space have caused many explorationists to conclude that phase shift methods are unsuitable for migrating seismic data from areas with complicated velocity structures (Berkhout, 1981). This is an unfortunate conclusion, given the frequent coincidence of steep dips with drastic changes in lateral velocity, particularly at the boundaries of salt structures. The need to provide accurate imaging of structures indigenous to these environments motivated the following investigation.
A mathematical development and error analysis of the split-step Fourier migration method were recently presented by Stoffa et al. (1990). In split-step migration, downward continuation of a single frequency component w of an exploding reflector wavefield P collected at a depth z is achieved by
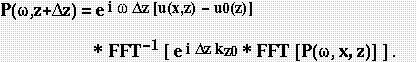(1)
In (1), u(x,z) is the medium slowness (inverse of velocity) as a function of position, u0(z) is the chosen reference slowness, and kz0 is the dispersion relation given by
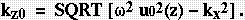
The symbols FFT and FFT-1 represent discrete forward and inverse Fourier transforms, and can be implemented on a computer using fast Fourier transform routines.
In a recent short note, Wenzel (1991) suggests an alternative Fourier migration which eliminates the need for a reference slowness. Wenzel's algorithm produces the downward continued wavefield at each x by evaluating all of wavenumber space with respect to each u(x,z). Using notation similar to equation (1), the operator suggested by Wenzel's equation 8 can be represented as
where
The Fourier migration scheme suggested here is a hybrid
of the Stoffa and Wenzel algorithms. As in PSPI migration
(Gazdag and Sguazzero, 1984), multiple reference slowness (MRS)
logic is utilized, but no interpolation is conducted. The
sequence of operations which compose the method can be
represented as
Equation (3) expands (1) to the MRS case, as denoted by j,
the new index on u0(z,j). Mu0(x,z) is the mapping function
between spatial position and reference slowness; each position
must be principally associated with one u0(z,j). As the
diversity of reference slownesses approaches that of the
discretely sampled slowness field, the method approaches
that of Wenzel.
A few observations can be made about algorithm efficiency
and operator order. The exponential operator outside the inverse
Fourier transform in (3) can be moved to the left side of the
delta function to reduce the number of calculations that are
necessary. More importantly, the algorithm should be capable
recognizing gaps and clusters in the distribution of the slowness
function. Algorithm efficiency can be greatly improved without
sacrificing accuracy if the distribution of the discrete slowness
function is considered when defining the reference slownesses.
A principal concern in implementing the MRS algorithm was
to avoid creating artifacts where a horizontal slowness gradient
is poorly represented by a discontinuity across widely spaced
reference slownesses. This can be achieved by insuring that,
when representing a gradient slowness function, the separation
between adjacent reference slownesses does not exceed some
maximum value. For the examples in this paper, the maximum
separation was constrained according to the ratio
This ratio was chosen on the basis of empirical testing of real
data examples. If the migration is run with a number of
reference slownesses which is insufficient for the slowness range
across a particular migration interval, the reference slownesses
are centered around the mean slowness at that depth, thereby
limiting the algorithm accuracy. The sufficient number of
reference slownesses needed to completely represent a migration
interval is given by
Figure 1 is the model for an impulse response test
developed by Swavek Deregowski of BP Exploration Company Ltd,
together with a superimposed ray trace solution. The model,
from left to right, consists of a vertical unit 750 meters
wide with a velocity of 2500 m/s, beside another vertical unit
750 meters wide at 3500 m/s, and then a 1500 meters wide
vertical unit with a velocity of 1500 m/s. Embedded in the
1500 m/s unit is an upright cone with steep flanks and a
velocity of 2500 m/s. The impulse response test involved
migrating eight spikes in this velocity field; four of the
spikes were located immediately below the point of the cone,
and the other four were 150 meters to the low velocity side of
the 2500-3500 m/s boundary. The ray trace solution is
incomplete because it does not include internal reflections;
also some events appear exaggerated because the algorithm does
not account for transmission losses across velocity boundaries.
The wavelet response of split-step Fourier migration
with one reference slowness was excellent, particularly for
high dips (Figure 2). Kinematically, though, response
mispositionings were significant. Figure 3 shows the results
of the impulse response test using 8 virtual reference
slownesses. Because only three reference slownesses are
required to represent the model, computation time only
increased by a factor of 2 over the one reference slowness
case. In Figure 3, both wavelet response and kinematic accuracy
are excellent.
The next example shows the results of the split-step
Fourier algorithm on real data. Figure 4 and Figure 5 are large
scale images of the flank of a salt diapir after migration.
Figure 4 was taken from a finite difference migration,
while Figure 5 was produced using the extended split-step
algorithm. The split-step migration operated over 2048
traces, and imaged the data to a depth of 7000 meters, using
a frequency band of 2 to 60 hertz. The migration interval was
12 meters, and the output sampling were used at each depth
interval. The migration required 1483 seconds of arithmetic
processor (AP) time on an NEC SX-3 supercomputer, or 2.8
times the AP time required when using one reference velocity.
The noisy quality of the image in Figure 4 is due to
dispersion introduced by the finite difference solution.
Although a steep dip extension had been added to the algorithm
the steep reflectors compromising the flanks suffer from
continuity problems because mispositioning occurs for reflectors
with dips above 65 degrees. By comparison, the image in Figure 5
shows good continuity of steep reflectors and the noise
content of the image is low. This performance is due to the
ability of the split-step Fourier algorithm to accurately
position high dip energy with relatively little frequency
dispersion.
A steep dip depth migration which accurately
handles severe lateral velocity variations was developed by
adding MRS logic to the split-step Fourier method. Properly
implemented, the method is computationally efficient for
either 2D or 3D migration. Migration of a 250,000 trace 3D
survey has been performed on an NEC SX-3 supercomputer in
an elapsed time of 30 hours, including SEGY format tape
input and output. Because the migration is a phase shift
implementation, it does not experience the dispersion and dip
limitation problems inherent in finite difference methods.
The author would like to thank Randy Carroll,
Swavek Deregowski and Pamela Gutteridge of BP Exploration for
their encouragement during the course of this work. Also,
the author thanks BP Exploration, Hamilton Bros.,
Murphy/Ocean, Fina, Lasmo, and Monument for permission to
publish the North Sea salt diapir.
This research was carried out as part of the 3D
consortium project at HARC. The author acknowledges the
support provided by the sponsors of this project.
Figure 1 :
Wedge model for impulse response test with superimposed ray trace
solution.
Figure 2 :
Impulse response of split-step Fourier migration using one
reference slowness on wedge model.
Figure 3 :
Impulse response of extended split-step Fourier migration on
wedge model.
Figure 4 :
Depth image of the flank of a salt diapir after steep dip
finite difference migration.
Figure 5 :
Depth image of the flank of a salt diapir after extended
split-step Fourier migration.
Figure 6 :
Depth image of the flank of a salt diapir after
split-step Fourier migration using one reference slowness per
migration interval.
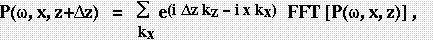
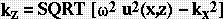. In equation (2), the data are
returned to spatial coordinates by a summation over all kx.
Therefore, although this method would produce none of the
inaccuracies associated with using reference slownesses, its
computational cost would be significantly more than that of the
Stoffa algorithm because of its more limited ability to use fast
Fourier transform routines.
MRS Migration
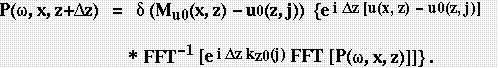(3)
Discussion
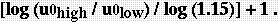
Examples
Conclusions
Acknowledgments
References
Gazdag, J., and Sguazzero, P., 1984, Migration of seismic
data by phase-shift plus interpolation: Geophysics,
v. 49, 124-131.
Stoffa, P. L., Fokkema, J. T., de Luna Freire, R. M., and
Kessinger, W. P., 1990, Split-step Fourier migration:
Geophysics, v. 55, 410-421.
Stolt, R. H., 1978, Migration by Fourier transform:
Geophysics, v. 43, 23-48.
Wenzel, F., 1991, Frequency-wavenumber migration in laterally
heterogeneous media: Geophysics, v. 56, 1671-1673.
Figures
