A solid body can be deformed by the application of an external force. If the solid is perfectly elastic, it will return to its original shape once that force is removed. In the context of exploration seismology, the earth can generally be considered as perfectly elastic because the stresses generated by seismic exploration activities are too small to permanently deform subsurface rocks. The elastic limit is the maximum stress that can be applied to a solid without permanently deforming it.
When an impulsive or transitory stress is applied to a finite area on the surface of an elastic solid, a strain is generated in the immediately adjacent subvolume. The strained subvolume then transfers stress to adjacent interior areas within the solid, which generates strains in surrounding subvolumes. In this fashion an impulsive stress propagates through a solid as an elastic wave. Elastic waves that propagate in the earth are known as seismic waves.
The exploration seismologist is primarily interested in seismic body waves that propagate through the earth's interior; however, seismic energy can also propagate as surface waves. Seismic surface waves are generally regarded as a form of noise in seismic exploration because they only contain information about the very near surface. For land reflection surveys, however, surface waves may have amplitudes that are significantly greater than the amplitudes of the sought after body waves. Also, depending on the depth of interest, these surface waves may arrive at the seismic sensors at nearly the same time as the desired signals. In these situations, suppression of surface waves during acquisition and/or their removal during processing become important considerations of the seismic experiment.
Seismic body waves can be subdivided into two distinct wave types on the basis of the direction of the seismic wave propagation relative to the direction that particles in the medium are displaced during propagation. For compressional waves, particles in the medium move parallel to the propagation direction. For shear waves, medium particles move perpendicular to the propagation direction. Within a medium, compressional waves propagate faster than shear waves. For this reason, compressional waves are usually referred to as primary waves, or P-waves, and shear waves are also referred to as secondary waves, or S-waves.
The seismic velocity of a medium is a function of its elasticity and can be expressed in terms of its elastic constants. For a homogeneous, isotropic medium, the seismic P-wave velocity Vp is given by
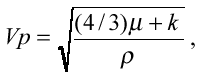
where
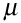is the shear modulus, k is the bulk modulus and 
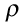is the density of the medium. Using the same notation, the S-wave velocity Vs is given by
As the names imply, the shear modulus is proportional to the shear strength of the medium, while the bulk modulus describes the incompressibility of the medium. The elastic constants have real values and are never negative, so a comparison of the expressions for Vp and Vs supports the observation that P-waves always travel faster than S-waves. Also, the expression for Vs implies that shear wave propagation can only be supported by solid bodies with shear strength. Fluids such as air and water do not support the propagation of S-waves. In any case, most seismic reflection surveys are exclusively concerned with P-wave acquisition, processing and interpretation.
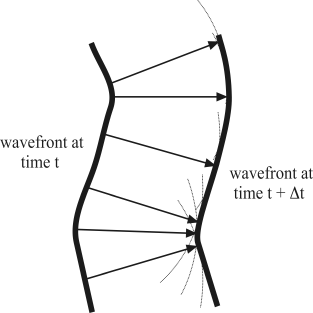
Figure 1: Huygen's Principle is a kinematic description for calculating the position of a wavefront at time (t + Dt) from the position of the wavefront at time t. Huygen's Principle does not address the amplitude of the wavefront.
Seismic wave behavior can sometimes be understood intuitively in terms of ray path theory. First, consider a wave front at a particular time t inside a medium of velocity V. (A wave front is a constant phase surface inside a moving wave.) According to Huygen's Principle, the location of the wave front at a later time (t + Dt) can be calculated by assuming that the wave front will advance by a distance V*Dt from each point along the current wave front. By using every point on the wave front at time t as the origin of an arc with radius V*Dt, the position of the wavefront at time (t + Dt) can be constructed from the envelope of the arcs. In other words, each point along the wavefront at time t acts as an independent wave source, and the wavefront at time (t + Dt) can be constructed by summing all the individual source contributions (Figure 1). A line segment from a point on the time t wavefront to the position where its arc touches the time (t + Dt) wavefront defines a raypath of the seismic wave. Note that the raypath is perpendicular to both wavefronts. A raypath that extends from a seismic source to a detector is referred to as a travel path.
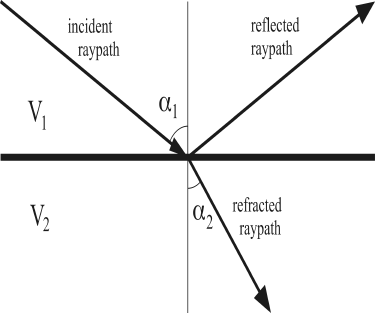
Figure 2: Refraction and reflection of a ray path at planer impedance boundary.
Two important concepts in seismic propagation are reflection and refraction. Figure 2 shows a two-layer model with a higher velocity layer over a lower velocity layer. In the figure, a down-going ray in the upper layer is partitioned into an up-going reflected ray and a down-going refracted ray at the layer boundary. For this simple homogeneous model, the raypath geometry can be specified by three principles: (1) raypaths in a constant velocity medium are straight. (2) At an impedance boundary, the reflected raypath is reflected at an angle equal to the angle of incidence. (3) At an impedance boundary, a change in velocity will cause the transmitted ray path to bend or refract. The refraction angle can be calculated using Snell's law, which is given by
where V1 and V2 are velocities in the upper and lower layers,
is the angle of the incident raypath with respect to the vertical, and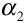 
is the angle of transmission of the refracted raypath with respect to the vertical. Note that Snell's law is also valid for the reflection angle if V2 on the right hand side of the equation is replaced by V1. Figure 2 is incomplete for the general elastic case because it neglects the phenomenon of seismic mode conversions. For the general case, each layer should have a P-wave velocity and an S-wave velocity. Then if the incident ray in the diagram represents a down-going P-wave, it will be partitioned into four waves at the layer boundary: a reflected P-wave, a refracted P-wave, a reflected converted S-wave and a refracted converted S-wave. The angles of reflection and refraction for the converted raypaths can also be calculated using Snell's law.
For the purposes of exploration geophysics, the local geology of a sedimentary basin can frequently be represented by a simple "layer-cake" model consisting of a stack of homogeneous rock layers with planar upper and lower surfaces. As was the case in Figure 2, all changes in density and acoustic velocity in a layer-cake model are assumed to occur at the layer interfaces. When a seismic wave encounters an interface, it is partitioned into a reflected wave that bounces off the interface and a refracted wave that crosses the interface, but may change its propagation direction.
Seismic velocities vary greatly with the type of rock or medium. P-wave velocities of sedimentary rocks range from 1500 m/s for water, to 4500 m/s for salt, and between 800 and 5000 m/s for sandstones. These materials, together with shales and carbonates, are the main components of the world's sedimentary basins. Oil and gas deposits are almost exclusively located in porous sedimentary rocks (such as sandstones and carbonates) and may be held in place by impermeable sedimentary rocks (such as salt and shale). Using seismic methods, it is usually possible to derive estimates of subsurface seismic velocities. Unfortunately, even perfect knowledge of the seismic velocity does not provide a unique identification of rock type. The seismic velocity of a sedimentary rock may vary depending on its fluid content, precise mineral composition, degree of compaction, and strength of cementation, among other factors; as a result, the velocity ranges of different rock types overlap.
