The traditional seismic processing sequence is cumbersome and detail-laden. To produce an interpretable seismic image of the subsurface, high power computers must apply numerous signal processing operations to enormous amounts of raw seismic data. The corrections applied by each processing operation typically vary with respect to location within the survey area, source event, source-receiver offset and time within the seismic trace. As a result, the seismic processor must usually perform a tedious analysis of the data set to select appropriate parameter variables for every processing operation. Rather than attempting a step-by-step description of a typical processing sequence, the following discussion will focus on three of its principle goals.

The first goal of seismic processing is to improve the temporal resolution of the seismic data. The convolutional model of reflection seismology defines a seismic trace as the convolution of an input seismic signal (the source) with an earth model composed of discrete reflectors. One objective of seismic processing, then, is to remove the character of the source from the data and obtain the idealized impulse response of the earth model; this process is known as deconvolution. If successful, each seismic trace is transformed into a time series of impulses or spikes with arrival times that represent primary or "one-bounce" reflection times to all reflectors, and amplitudes that represent the reflection coefficients of the reflectors. A number of propagation effects must be removed to make the data mimic the impulse response model; these include reverberations of the source signal, source and receiver ghosts, or reflections, from the air-water interface, and multiples in the seismic data from wavefronts that have undergone more that one subsurface reflection. Some of the deconvolution and multiple suppression operations applied during a typical processing sequence include frequency filtering, spiking deconvolution, predictive deconvolution and multichannel filtering of coherent noise.

A second goal in seismic data processing is to improve the low signal-to-noise quality typical of seismic data. In acquisition, this is the primary motivation in deploying as many receivers per shot as feasible and collecting data that are redundant to some degree. These "excess" data are traditionally processed using the common mid-point, or CMP, method (sometimes inaccurately called the common depth point method). In CMP processing, seismic traces are grouped into CMP gathers on the basis of shared source-receiver midpoint bins (Figure 4). Velocity functions are calculated for selected CMP gathers based on arrival time variations as a function of source-receiver offset for a few reflection events in the gather. CMP velocity functions are then interpolated throughout a survey area to construct a velocity model of the subsurface. This velocity model is used to perform normal move-out (NMO) corrections throughout the survey. NMO is a non-linear stretching of the seismic time axis to remove the travel time component due to source-receiver offset. NMO is applied to each trace in a gather so that the reflection travel times on all traces approximate that of a trace with zero source-receiver offset (a coincident source and receiver). After NMO, all the traces in a CMP gather can be summed, or stacked. If the subsurface geology does not violate the assumptions of the CMP method too strongly, reflection events on the different traces will sum constructively, producing a single trace with a signal-to-noise ratio that is much higher than that of the individual prestack traces. By repeating this procedure for all CMP gathers in the survey, the prestack data set is replaced by a much smaller poststack data set of much higher signal quality.

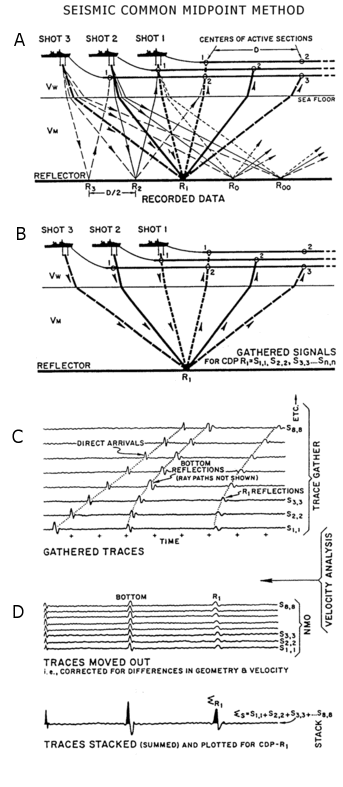
Figure 4: (A) Various raypaths from successive shot locations to the active streamer elements. (B) For a horizontal reflector beneath a stratified velocity structure, rays from source-receiver pairs with a common midpoint will be reflected from a common depth point on the reflector. (C) Seismic traces corresponding to these rays plotted along horizontal lines constitute a CMP gather. The direct arrivals, the seafloor reflections and (assumed) subsurface reflections at one interface are shown. The seafloor and subsurface reflections for different traces lie along curves that are hyperbolic or close to hyperbolic for the simplest crustal geometries. (D) To sum the traces in a single gather, an NMO correction is applied. If the traces lie along hyperbolas, a single velocity function (for each reflector) can be derived and applied. This velocity is known as a stacking velocity. The traces can then be summed. (E) The summed traces constitute a stack section. Modified from Talwani M., Windisch C.C., Stoffa P.L., Buhl P. and Houtz R.E., 1977, Multichannel seismic study in the Venezuelan Basin and the Curaco Ridge. In Talwani M. and Pitman W.C. III eds. Island Arcs, Deep Sea Trenches and Back-Arc Basins. Maurice Ewing Series 1, pp. 83-98, American Geophysical Union.

The CMP method has been highly successful in seismic data acquisition and processing. Since the early 1960's, nearly all reflection seismic surveying has been based on the CMP method. However, the CMP method explicitly assumes two rather severe oversimplifications: that the seismic velocity is constant and that all subsurface reflectors are horizontal. Dip move-out (DMO) is a processing operation that preconditions prestack data for CMP processing by correcting for the effects of dip. DMO processing has greatly extended the accuracy and usefulness of the CMP method for areas where the geology violates the assumptions of the method.

A third goal of seismic data processing is to improve the lateral resolution of the seismic data. CMP processing produces seismic stack sections or volumes in which every surface position is represented by a single seismic trace. When displayed, the stack appears to be a geological image. The image is imperfect, however; the seismic wavefield was distorted by diffractions and spherical spreading as it propagated through the subsurface. To produce an image that is more readily interpretable, the seismic data can be transformed into a subsurface image by means of seismic migration. Migration is an inverse wave scattering calculation that relocates seismic reflections and diffractions to the location of their origin. Because migration arranges data laterally in the image volume, it is inherently a 2-D or 3-D procedure, unlike the mostly one-dimensional procedures that were described above. For complicated three-dimensional structures, 3-D migration produces a more accurate seismic image than 2-D migration. Of course, 3-D migration can only be applied to data acquired during three-dimensional surveys. When a two dimensional survey is collected over complicated structures, much of the seismic energy that is recorded within the seismic profile is actually reflected from out-of-plane reflectors (the plane is the vertical section underlying the profile). If 3-D data are available, 3-D migration can be used to remove this energy from the profile and to restore energy that was reflected from inside the plane but recorded on a different profile.

Each trace of a stacked seismic data set is produced by summing seismic traces that share the same source-receiver midpoint coordinate. As can be seen from Figure 4, proper stacking depends on appropriate NMO functions being applied to all common midpoint gathers so that the delay times of reflection events line up. NMO corrections usually assume the uncorrected reflection events lie along hyperbolic curves. This is strictly true only if the earth is a constant velocity medium above the reflector; for layered media it is approximately true. For complex structures, the events may not lie on a hyperbola and therefore will not move-out and stack properly. Events can also appear on CMP gathers at the same travel time, but with different stacking velocities. In such cases, it is necessary to perform migration on the individual seismic traces before rather than after stacking. Prestack migration simultaneously improves both the lateral resolution and the signal-to-noise quality of seismic image; all the data contained in the individual traces are available during imaging, whereas stacking may destroy information that only appears at certain offsets. Prestack migration thereby replaces the functions of both stacking and poststack migration. In current practice, however, CMP processing is routinely applied before the data are reprocessed using prestack migration. Prestack migration has obvious advantages over poststack migration, but also some disadvantages. A disadvantage of prestack migration is the size of the prestack data volume that must be migrated. If a gather contains 100 traces, the data volume for prestack migration is 100 times larger than the equivalent volume for poststack migration. For 3-D data sets, the increase in data size makes enormous demands on computer speed and memory.

One important characteristic of both the CMP method and prestack migration is that a by-product of both procedures is the generation of a subsurface velocity model. Although I did not include derivation of the velocity model as a processing "goal," it has obvious interpretational importance. In prestack migration, velocity analysis algorithms allow processors to improve their velocity models between migration iterations. Prestack migration programs which produce a migrated offset gather at each CMP location are particularly useful for certain velocity estimation strategies. These common image gathers, or CIGs, allow the processor to perform velocity analysis using relatively familiar methods.

Besides distinctions between 2-D versus 3-D, and poststack versus prestack, migration implementations are also distinguished as either time migrations or depth migrations. Time migration assumes that, locally, the variations in velocity are a function of depth alone. Also, time migration usually ignores the refraction that occurs when rays cross velocity boundaries. When large lateral velocity variations occur, whether they are within a layer or whether they involve layer boundaries, time migration may result in significant mispositionings of the reflectors. The advantage of time migration lies in the fact that the migration algorithms are simple and thus require less computer performance and memory. However, where structures are complex and large variations in lateral velocity occur, depth migration is necessary. Depth migration uses an input velocity model to calculate ray refractions as part of deriving the subsurface image. It requires more computer performance than time migration, and the quality of the depth migration is more sensitive to the accuracy of the velocity model that is employed. Determining an appropriate velocity model is difficult, but the situation is ameliorated by the fact that a preliminary model can be iteratively improved. Because defining a depth velocity model is inherently an interpretative function, depth migration blurs the division between processing and interpretation.

Although basic principles of seismic data processing were described here, a number of common and important operations in seismic data processing were not covered. These include trace editing, muting, correction for spherical divergence, gain application and statics corrections. Processing requirements for individual seismic surveys may differ greatly. A seismic data processor needs to exercise creativity and flexibility in designing the processing sequence to address specific problems and goals.